Lynn Margulis, the mother of all holobionts.
The concept of holobiont has several definitions, the simplest one being "any symbiotic system." But that definition tells us little of what makes holobionts tick and it is often arbitrarily limited to microbial systems. The concept of "holobiont" is wider, and it is based on a functional definition: a holobiont is anything that behaves as a holobiont, that is, in terms of the interactions among the creatures that compose it. Here, the master trick is symbiosis, intended as a win-win interaction extended at the network level. In holobionts, all creatures are linked to each other (directly or indirectly) in a network of interactions that involve advantages for all the creatures involved. Holobionts are the result of natural selection that favors those holobionts that can obtain homeostasis -- the stability that allows them to survive and, hence, win the evolutionary game.
But how is this win-win mechanism? It is best explained by an example. Many kinds of systems, even non-biological ones, can function in the same way as microbial holobionts. So, the simplest network I can think of as an illustration of the holobiont mechanism is a flock of birds. Every bird communicates visually with other birds. There are several fascinating models of how bird flocks fly, but here let's see an even simpler system: birds foraging in a field. One bird sees something suspicious, it flies up, and in a moment, all the birds are flying away. There you go:
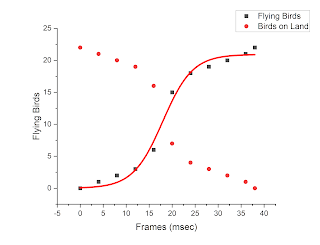
You can see in the figure the fitting of the number of flying birds as a function of time using a logistic function.
The mechanism of this interaction is simple: one bird detects a predator and flies away. The message arrives to all the other nodes of the bird network as a "
meme" a basic unit of communication. The meme "a predator is nearby" spreads all over the network and rapidly all birds fly away. Note that the bird that sees a predator acts only in view of its own survival: it does what it would do if alone. But all birds benefit from the bird acting as a "sentinel." It is a win-win strategy. Incidentally, human beings tend to do the same. A human crowd has two basic states: "calm" and "stampede." But even humans can be said to have just two states according to the principle proposed by James Schlesinger: complacency or panic.
Let's try now to model this behavior. We can use the "SIR" (susceptible, infected, removed) model, well known in epidemics. We call "
S" the number of "normal" members of the bird population,
I the number of panicked ones that flew away.
R is the number of birds that recovered from panic and alighted again.
Here are the equations of the SIR model:
S'=- k1SI
I'= k1SI-k2I
The apostrophe symbol indicates the first derivative with respect to time. The k(s) are positive constants. There is a third equation for R, but we don't need to write it since R' is simply equal to k2I.
This system doesn't have an analytic solution, but it can be easily solved iteratively. The result is the typical bell-shaped curve observed when an epidemic flares in a population.
Note how not the whole population is infected; a fraction remains untouched. They have a "natural immunity" -- in this case a memetic immunity. This fraction can be calculated as approximately equal to k2/k1 (take the second derivative of S, and approximate I =0 for t>>0). The meme will diffuse more the larger the diffusion factor, k2, but that will be hampered by the decay factor, k3.
The system is evolutionary. The k2/k1 ratio is calibrated in such a way as to optimize energy consumption: every bird that flies consumes a certain amount of metabolic energy that has to be compared with the energy that the flock would lose if one or more birds were not to fly.
In general, for a flock of birds, the k2/k1 ratio is large, but it doesn't mean that all birds immediately fly away when they receive the "predator" meme. See this clip (featuring my grand-daughter, Aurora):
You see that pigeons in a public park are much more difficult to scare than wild birds in the open. They have learned that humans aren't so dangerous, so the meme "a predator is here" doesn't generate the same quick flight response as the other video above. It is a case of "memetic herd immunity."
These are just initial notes on how the concept of "holobiont" is strictly linked to the network structure that creates it. Some network structures are much more complex than the simple "lattice" ones formed by a flock of birds or a herd of herbivores. A general theory that classifies these structures is the "
Integrated Information Theory" (IIT) proposed by Giulio Tononi and others as an explanation of the phenomenon called "consciousness."
Personally, I am not sure if consciousness can be measured in terms of the "phi" function proposed by Tononi, but the idea has interesting applications with holobionts since it deals with how many states a network can have. A flock of birds can have just two states, a human brain... well, let's just say a large (hugely large) number. So, holobionts could be classified in terms of their Phi value according to IIT. But this is a complicated subject that deserves to be discussed in more detail in another post.